Blažej Bucha

Lecturer at the Department of Theoretical Geodesy and Geoinformatics, Slovak University of Technology in Bratislava.

This page offers outputs from some of the research papers that I co-authored, all of them being related to gravity field modelling. The computer codes are written in C, Fortran and/or MATLAB. Anyone is encouraged to tailor the routines as freely as needed.

In case you have any comments, suggestions, questions or criticism, please feel free to contact me at blazej.bucha@stuba.sk. If you too prefer secure communication, you may want to sign your email and/or encrypt it with my public_key using GNU Privacy Guard. The key fingerprint is EF9A 8C56 E625 8A23 A844 EFB3 24DD 5C83 468E 5E30.

GitHub: https://github.com/blazej-bucha
ResearchGate: https://www.researchgate.net/profile/Blazej-Bucha

Contents

• GrafLab — High-degree surface and solid spherical harmonic synthesis


• isGrafLab — High-degree solid spherical harmonic synthesis at regular grids residing on irregular surfaces


• GOCE-only global gravity field models from the kinematic orbit


• Divergence-free spherical harmonic gravity models of the Moon's topographic masses


• SRTM2gravity — Near-global 3 arcsec maps of topography-implied gravity


• CHarm — C/Python library for spherical harmonic transforms


• Molodensky's truncation coefficients for cap-modified spectral gravity forward modelling


• SRBF_package for gravity field modelling with spherical radial basis functions


• GMSQ2019 — 2 arc-sec gravimetric quasigeoid of Slovakia


• grav-sr-2arcsec — A suite of 2-arcsec surface gravitational maps of the Slovak Republic up to the full gravitational tensor


• GFM_DE_rule package for spatial-domain Newtonian integration


• Asteroid Bennu — Spherical harmonic models of Bennu's gravitational field


• Publications


• Presentations


• Posters


• Teaching


• Favourite websites

GrafLab

OVERVIEW
--------
Name: GrafLab
Description: Package for high-degree spherical harmonic synthesis
Programming Language: MATLAB
Version: 2.1.4
Updated: Mar 24, 2020
Download: https://github.com/blazej-bucha/graflab
Cookbook: https://github.com/blazej-bucha/graflab-cookbook

GrafLab (GRAvity Field LABoratory) is a MATLAB-based routine to compute functionals of the geopotential up to high degrees (tens of thousands and beyond).

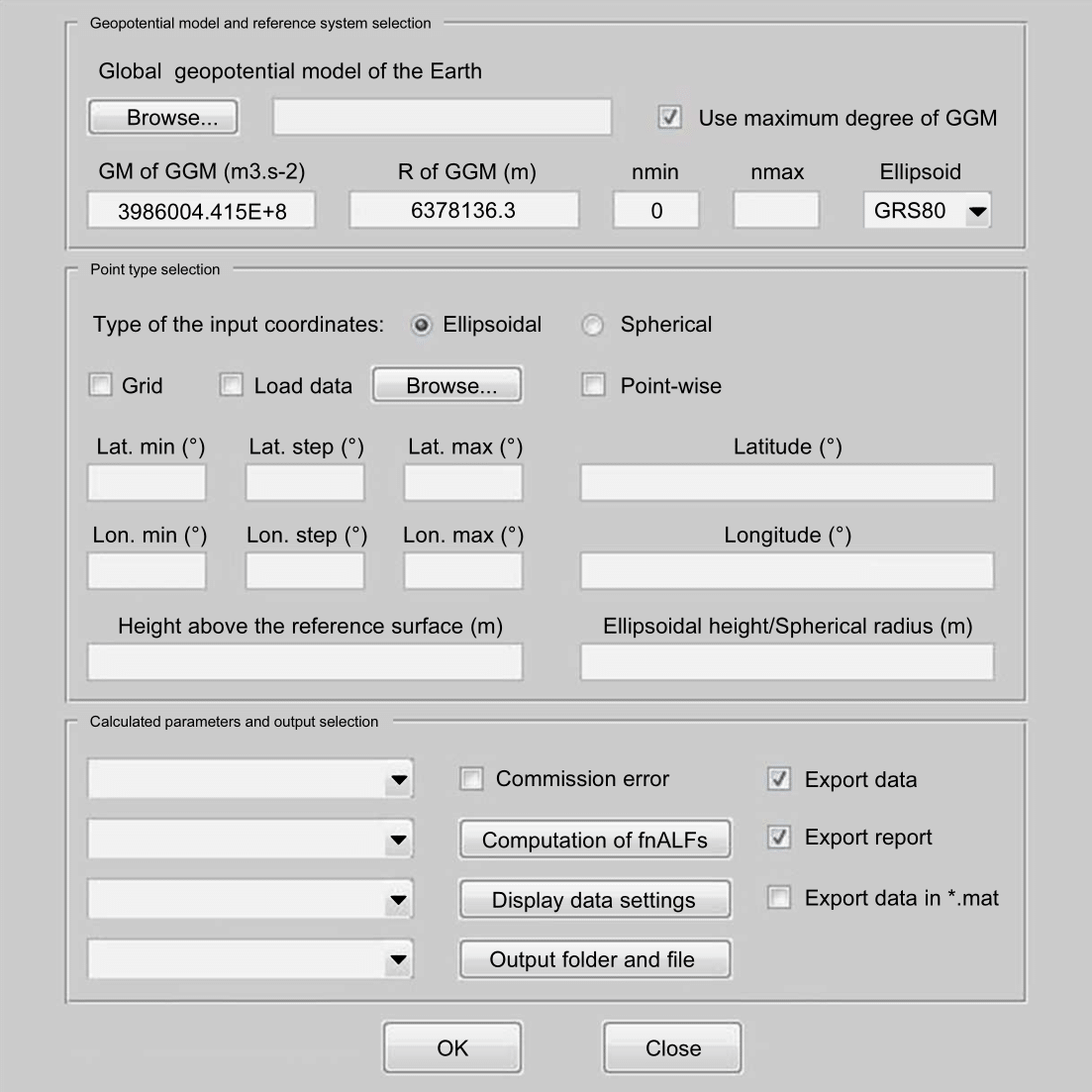
Features

• Evaluates 38 functionals of the geopotential (e.g., the geoid, height anomaly, gravity anomalies/disturbances, deflections of the vertical, gravitational tensor).
• Evaluates the commission error of 26 functionals using a full variance-covariance matrix of spherical harmonic coefficients.
• Supports efficient FFT-based synthesis at grids and point-by-point synthesis at scattered points.
• Reads models in the gfc format defined by ICGEM.
• Works with evaluation points defined by spherical as well as ellipsoidal coordinates.
• Plots output data on a map.

A user can interact with GrafLab either through a GUI (the figure below) or from the command line.

GrafLab was published in

Bucha, B., Janák, J., 2013. A MATLAB-based graphical user interface program for computing functionals of the geopotential up to ultra-high degrees and orders. Computers & Geosciences 56, 186-196, http://doi.org/10.1016/j.cageo.2013.03.012.

Please use this reference in your works when using GrafLab.

Some sample outputs from GrafLab

• Geoid undulations:

  

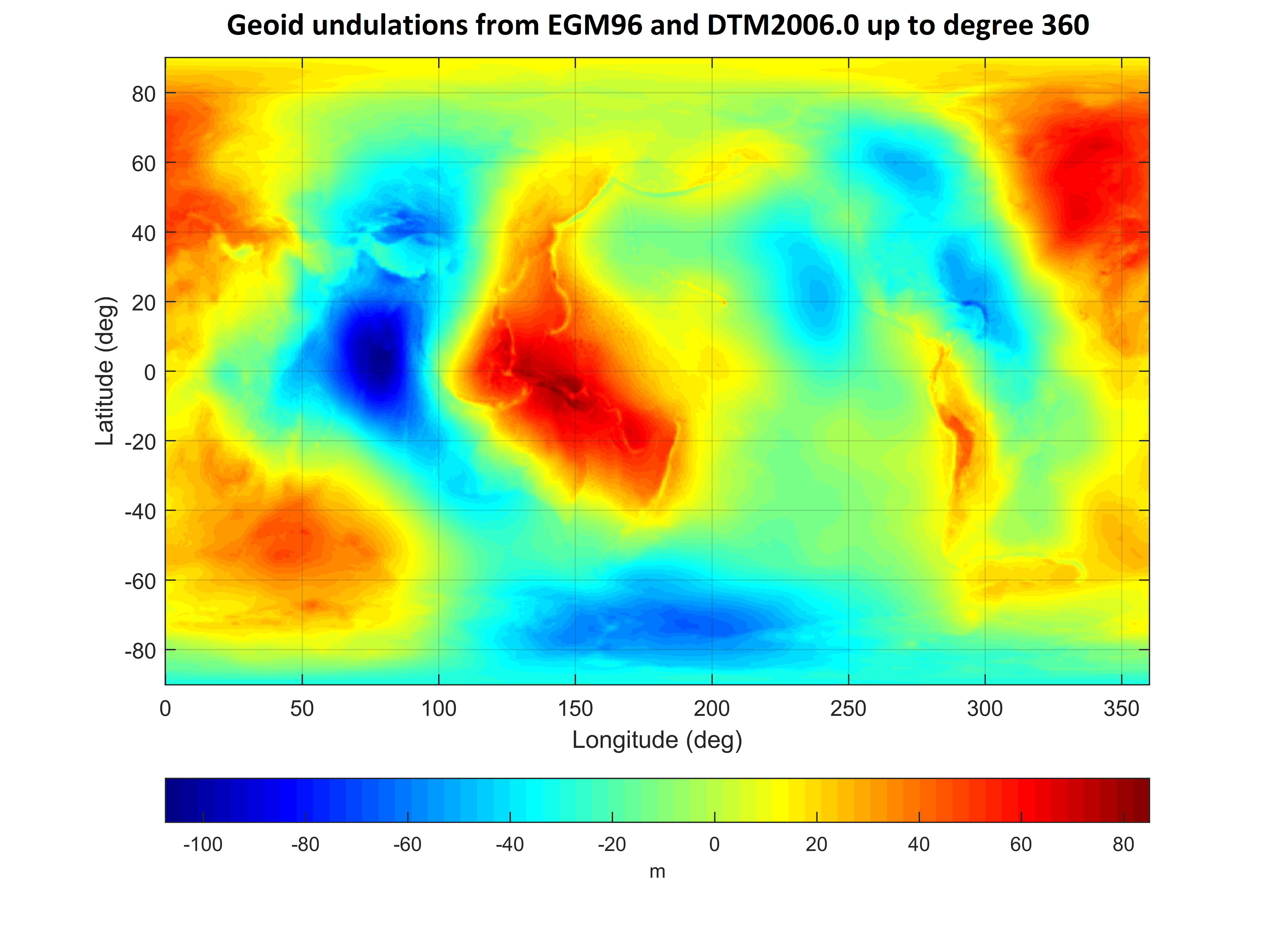
  This output can be reproduced by the following command (input data are provided inside the GrafLab repository):

  GrafLab('OK',3986004.415E+8,6378136.3,0,360,1,'EGM96.mat',0,0,-90,0.25,90,0,0.25,360,0,[],[],[],[],'EGM96_Geoid_to360',0,10,1,'DTM2006.mat',0,1,1,2,6,1,60,600,1)

• Planetary topographies (look for the text "Some useful tips and tricks" in the NEWS file inside the GrafLab repository):

  

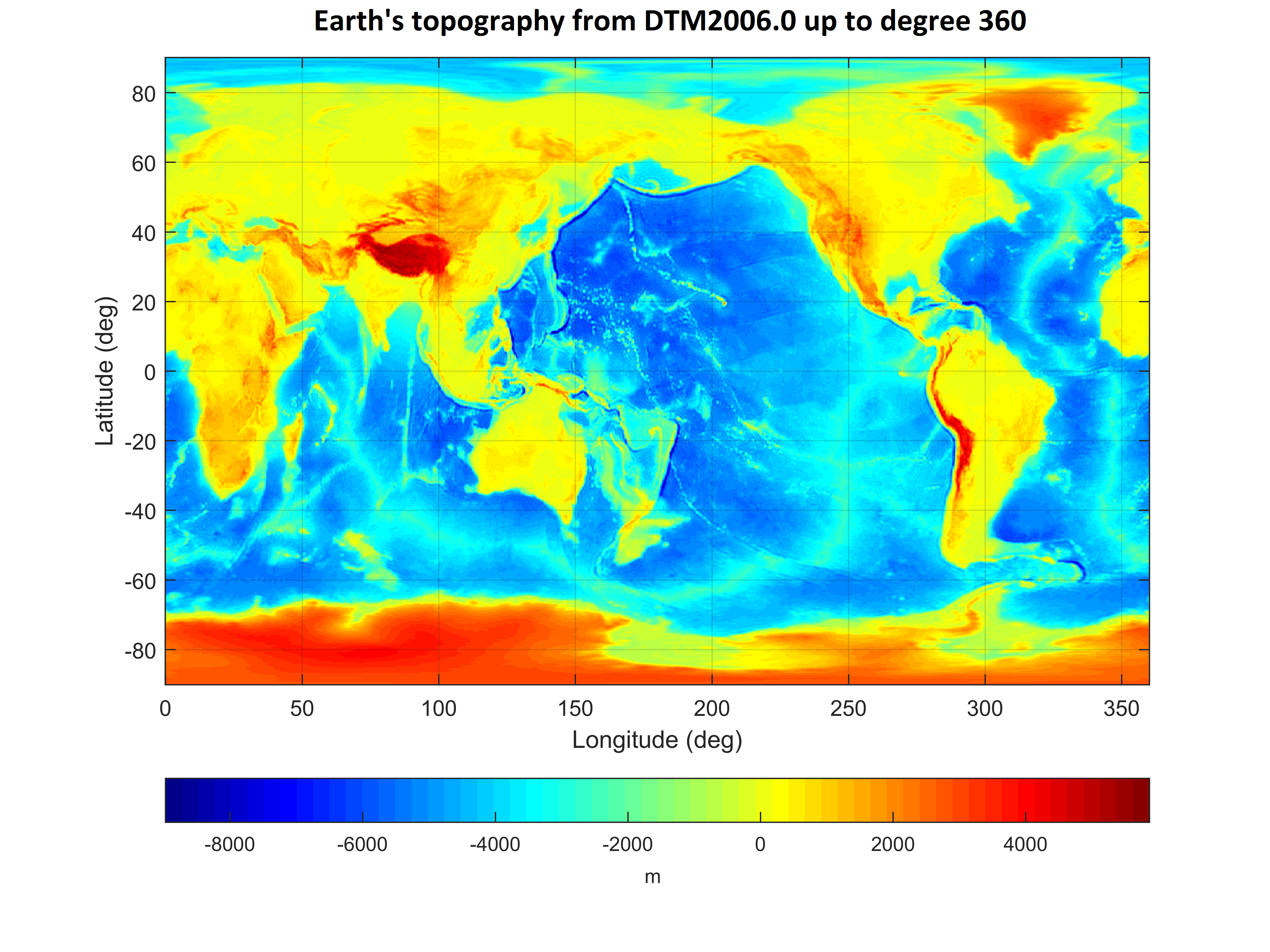
  This output can be reproduced by running the command (data inside the repo):

  GrafLab('OK',1,1,0,360,[0 0 0 0 0],'DTM2006.mat',1,0,-90,0.25,90,0,0.25,360,0,[],[],[],[],'Topography',0,11,1,[],0,1,1,2,6,1,60,600,1)

In fact, this command can perform any surface spherical harmonic synthesis of the form $$f(\varphi,\lambda) = \sum_{n=0}^{n_{\max}} \sum_{m=0}^{n} \left( \bar{C}_{nm}\, \cos(m\, \lambda) + \bar{S}_{nm}\, \sin(m\, \lambda) \right) \bar{P}_{nm}(\sin\varphi)\,,$$ $$f(\varphi,\lambda) = \sum_{n=0}^{n_{\max}} \sum_{m=0}^{n} \Bigl( \bar{C}_{nm}\, \cos(m\, \lambda)$$ $$ + \bar{S}_{nm}\, \sin(m\, \lambda) \Bigr) \, \bar{P}_{nm}(\sin\varphi)$$ where $\bar{C}_{nm}$ and $\bar{S}_{nm}$ are $4\pi$-fully-normalized (real) surface spherical harmonic coefficients of the function $f$, $n$ and $m$ are spherical harmonic degree and order, respectively, $\bar{P}_{nm}(\sin\varphi)$ are the $4\pi$-fully-normalized (real) associated Legendre functions of the first-kind, and, finally, $\varphi$ and $\lambda$ are the spherical latitude and longitude, respectively. This means GrafLab can synthesize a wide range of (real) functions given on a sphere up to high harmonic degrees (tens of thousands and beyond).

• Gravity field of celestial objects (look for the text "Some useful tips and tricks" in the NEWS file inside the GrafLab repository). As an example, shown below is the gravitational vector induced by topographic masses of the Moon.

  

  

  

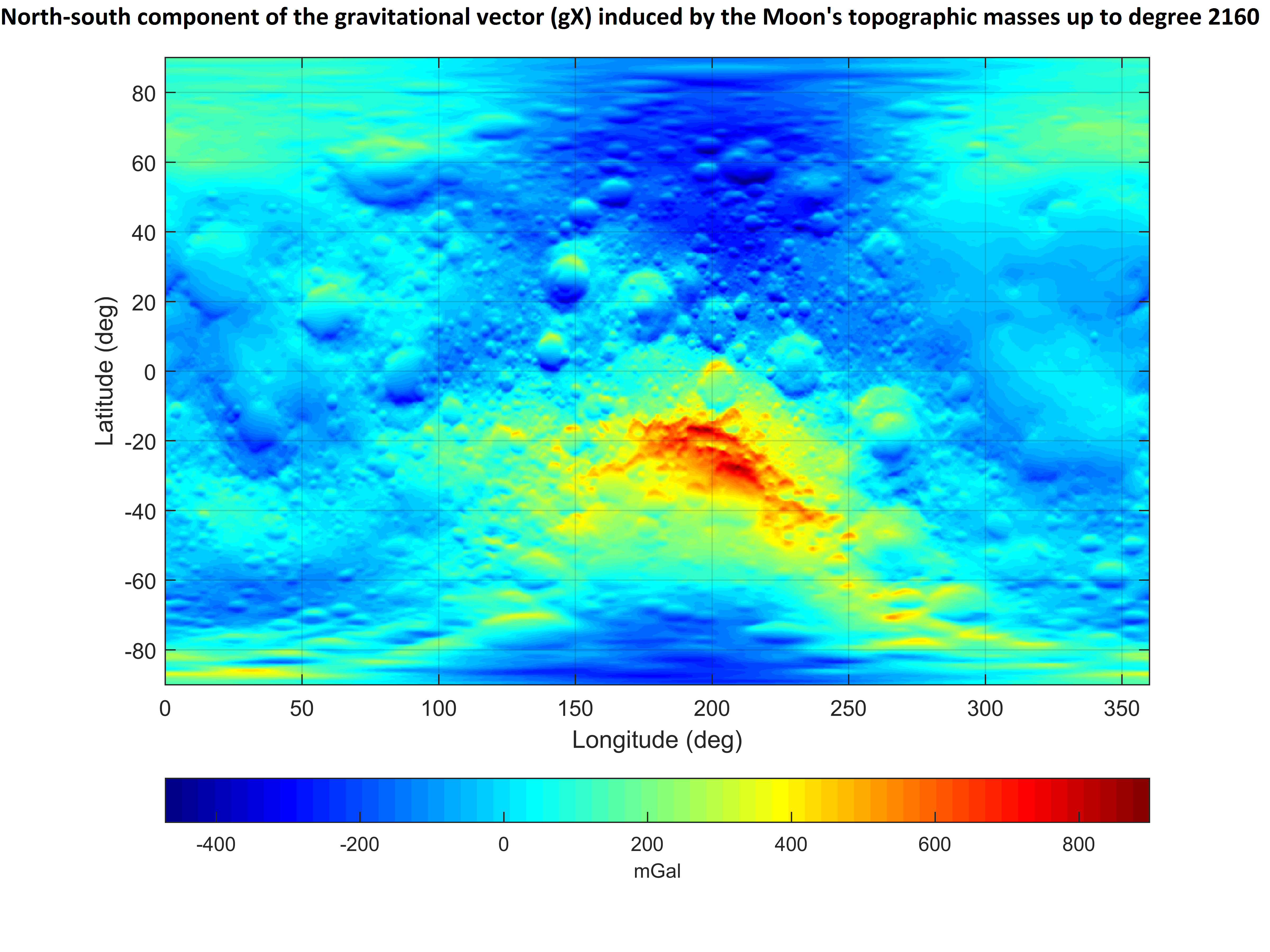
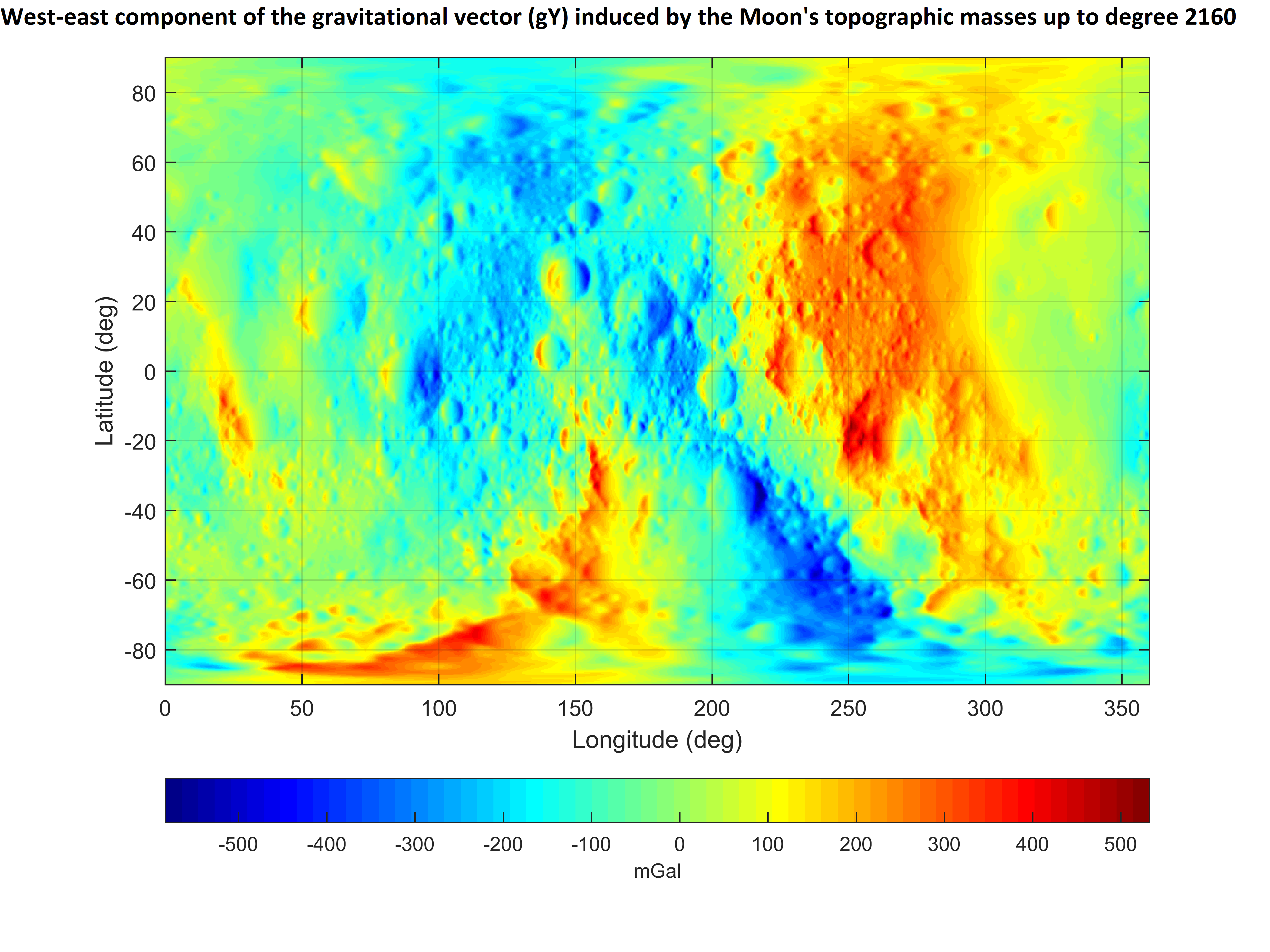
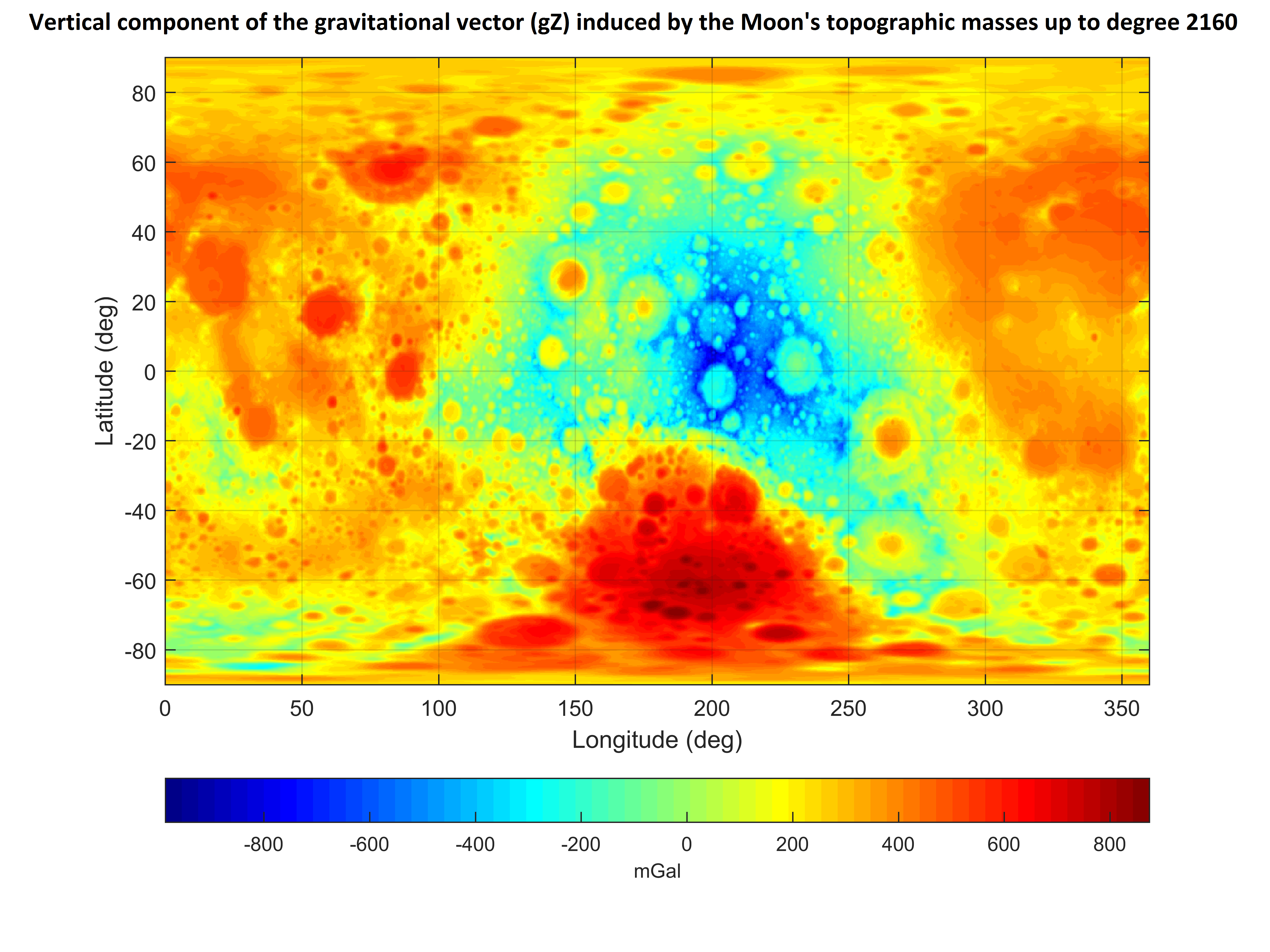
  The gravitational vector was computed up to degree 2160 at 5 arc-min grid from the model "STU_Moon_topography_to720_gravity_to2160.gfc" (see the section on divergence-free gravity models of the Moon's gravity field below) using the command:

  GrafLab('OK',0.4902805823000e+13,0.1737999e+07,0,2160,[0 0 0 0 0],'STU_Moon_topography_to720_gravity_to2160.gfc',1,0,-90,0.08,90,0,0.08,360,11000,[],[],[],[],'Moon_gravitational_vector',0,16,3,[],0,1,1,2,6,1,60,600,1)

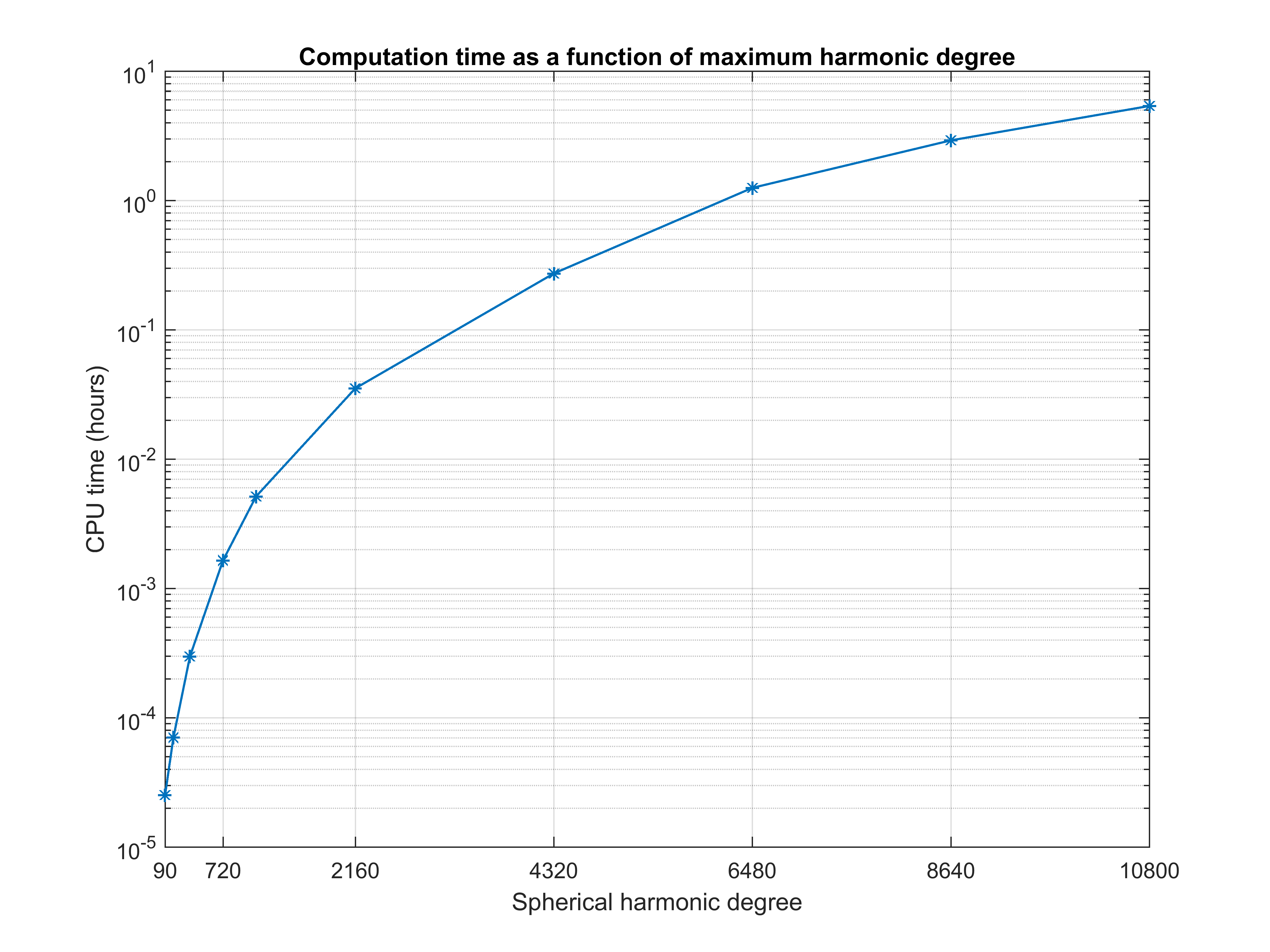
Computation time

Below are shown computation times required by GrafLab to synthesize the Earth's topography as represented by Earth2014.TBI2014.degree10800 up to harmonic degrees nmax = 90, 180, 360, 720, 1080, 2160, 4320, 6480, 8640 and 10800. The position of evaluation points is defined by the Gauss—Legendre quadrature. The dimensions of the grids are (nmax+1)*(2*nmax+2) in terms of the latitude and the longitude, respectively, and Legendre's functions were evaluated after Fukushima (2012). The tests were conducted on a PC with Intel® Core^TM i7-6800K CPU.

isGrafLab

OVERVIEW
--------
Name: isGrafLab
Description: Package for efficient high-degree spherical harmonic synthesis on irregular surfaces
Programming Language: MATLAB
Version: 2.1.3
Updated: Nov 8, 2019
Download: https://github.com/blazej-bucha/isgraflab
Cookbook: https://github.com/blazej-bucha/graflab-cookbook

isGrafLab (Irregular Surface GRAvity Field LABoratory) is a modified version of GrafLab that allows accurate and fast computation of functionals of the geopotential at dense grids residing on irregular surfaces such as the Earth's surface. It employs the efficient lumped coefficients approach for surface spherical harmonic synthesis of the functionals and their radial derivatives at regular surfaces (sphere or ellipsoid of revolution), and the Taylor series expansions to continue the functionals to the irregular surface.

Further details can be found in the paper:

Bucha, B., Janák, J., 2014. A MATLAB-based graphical user interface program for computing functionals of the geopotential up to ultra-high degrees and orders: Efficient computation at irregular surfaces. Computers & Geosciences 66, 219-227, http://doi.org/10.1016/j.cageo.2014.02.005.

Please use this reference in your works when using isGrafLab.

GOCE-only global gravity field models from the kinematic orbit

OVERVIEW
--------
Name: STU_GOCE_R1.zip
Description: GOCE-only spherical harmonic models of the Earth's gravitational field
Download: https://doi.org/10.5281/zenodo.7078125

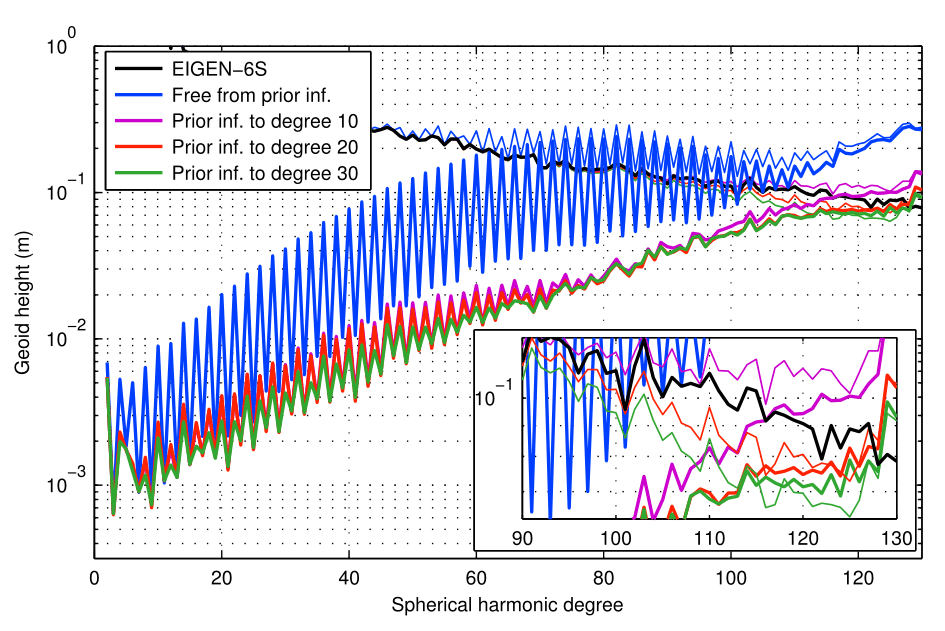
The models were estimated from the kinematic orbit of the GOCE satellite (01 November 2009 to 11 January 2010, the R1 period). Further details:

• the models were derived by spherical radial basis functions (Shannon SRBF) and subsequently they were transformed into spherical harmonics after the evaluation; the transformation is exact without any approximations,
• the acceleration approach was used to invert the kinematic orbit into the gravity field models,
• the problematic near-zonal coefficients (polar gap) are stabilized by prior information obtained from our own low-degree GOCE-only models, so that the final models are still GOCE-only,
• the models are estimated up to relatively high harmonic degrees (75, 100, 130) to mitigate the aliasing, but it is not recommended to use them beyond degree, say, 70 due to the adverse signal-to-noise ratio,
• the models are provided in the gfc format as defined by ICGEM (International Centre for Global Earth Models).

The effect caused by the stabilization of the near-zonal coefficients is shown in the figure below (Bucha et al., 2015).

When using the models, please use the following reference:

Bucha, B., Bezděk, A., Sebera, J., Janák, J., 2015. Global and regional gravity field determination from GOCE kinematic orbit by means of spherical radial basis functions. Surveys in Geophysics 36, 773-801, http://doi.org/10.1007/s10712-015-9344-0

Divergence-free spherical harmonic gravity models of the Moon's topographic masses

OVERVIEW
--------
Name: STU_MoonTopo.zip
Description: Spherical harmonic models of the gravitational field implied by the Moon's topographic masses
Download: https://doi.org/10.5281/zenodo.7078795

These models approximate the gravitational field induced by topographic masses of the Moon and mitigate the divergence effect of spherical harmonics in the vicinity of the Moon's topography. The models rely on the Runge—Krarup theorem and enable generally a more accurate evaluation of gravity field quantities close to the lunar topography as compared to the models from spectral gravity forward modelling. This is because the latter ones may suffer from the divergence effect when evaluating the spherical harmonic series on or below the limit sphere encompassing all the gravitating masses (that is, also on the topography). In the figure below, the two approaches are validated with respect to a third (reference) one (Bucha et al., 2019). The upper map shows the reference signal, the middle one depicts the differences related to the Runge—Krarup solution and the bottom one validates the spectral gravity forward modelling technique; note the different colour bars.

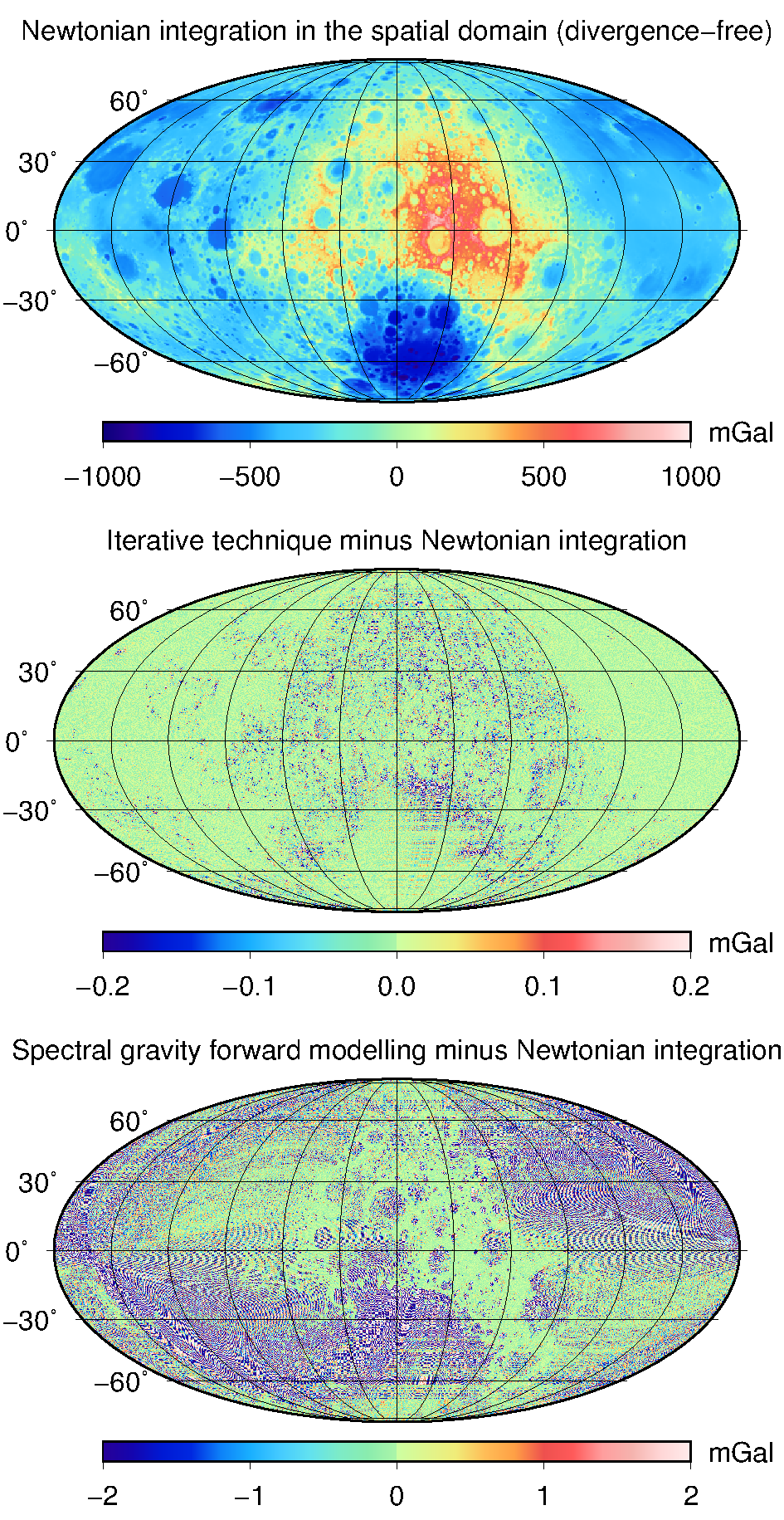
We provide 12 models that approximate the gravity field implied by the lunar topographic masses. The topographic masses are expanded up to degrees 90, 180, 360 and 720, and the maximum degree of the gravity field models varies from 360 up to 2160. All models are available in the gfc format as defined by ICGEM. One of the models, "STU_Moon_topography_to720_gravity_to2160", can also be accessed from ICGEM, where it can be find under a shortened name "STU_MoonTopo720".

The corresponding models that may suffer from the divergence effect were derived by Hirt and Kuhn (2017) and can be downloaded here, including grids of reference gravity disturbances from spatial-domain Newtonian integration.

Please use the following reference when using the models in your works:

Bucha, B., Hirt, C., Kuhn, M., 2019. Divergence-free spherical harmonic gravity field modelling based on the Runge—Krarup theorem: a case study for the Moon. Journal of Geodesy 93, 489-513, https://doi.org/10.1007/s00190-018-1177-4

SRTM2gravity — Near-global 3 arcsec maps of topography-implied gravity

OVERVIEW
--------
Name: SRTM2gravity
Description: Near-global 3 arcsec maps of topography-implied gravity
Authors: Christian Hirt et al.
Publication: https://doi.org/10.1029/2019GL082521
Download: https://ddfe.curtin.edu.au/models/SRTM2gravity2018/ or https://ddfe.blazejbucha.com/models/SRTM2gravity2018/
Academic Torrent: https://academictorrents.com/details/9eca33223c8b37b7b0ec44355e1abfb812fd43f9

For details on SRTM2gravity, visit https://www.asg.ed.tum.de/en/iapg/forschung/schwerefeld/s2g/.

CHarm — C/Python library for spherical harmonic transforms

OVERVIEW
--------
Name: CHarm
Description: C/Python library for high-degree spherical harmonic transforms
Programming Language: C, Python
Source Code: https://github.com/blazej-bucha/charm
Documentation: https://www.charmlib.org

CHarm is a C library to work with spherical harmonics up to almost arbitrarily high degrees. The library is accompanied by a Python wrapper called PyHarm.

Features

• Supports real-valued fully-normalized surface and solid spherical harmonics (the geodetic norm).
• Performs FFT-based surface spherical harmonic analysis and solid spherical harmonic synthesis with minimized memory requirements.
• Stable up to high degrees and orders (tens of thousands and beyond).
• Available in single, double and quadruple precision.
• Supports point and mean data values (both analysis and synthesis).
• Supports synthesis at grids and at scattered points/cells. Grid-wise computations are done by FFT whenever possible. If FFT cannot be applied, the less efficient Chebyshev recurrences are used along the latitude parallels instead.
• Computes the full first- and second-order gradients at evaluation points (e.g., the gravitational vector and the gravitational tensor).
• Supports the Gauss--Legendre and Driscoll--Healy quadratures.
• Integrates solid spherical harmonic expansions (e.g., of the gravitational potential) on band-limited irregular surfaces (e.g., on the Earth's surface). This routine is unique to CHarm and cannot be find in any other publicly available library.
• Computes Fourier coefficients of fully-normalized associated Legendre functions of the first kind up to high harmonic degrees.
• Supports OpenMP parallelization for shared-memory architectures.
• Supports AVX, AVX2 and AVX-512 SIMD CPU instructions to improve the performance.
• Performs discrete FFT by FFTW.
• Ships with a Python wrapper to enable high-level programming while retaining the efficiency of the C language. The wrapper, called PyHarm, wraps CHarm using ctypes and is fully integrated with NumPy.

The predecessor of CHarm, the SHA_SHS package written in C, Fortran and MATLAB, is archived here. The package works correctly, has its own brief documentation, but is no longer maintained.

Molodensky's truncation coefficients for cap-modified spectral gravity forward modelling

OVERVIEW
--------
Description: Molodensky's truncation coefficients for cap integration in spectral gravity forward modelling
Download coefficients: https://doi.org/10.5281/zenodo.7092048
Download source code: https://github.com/blazej-bucha/sgfm-qnpkj

Cap-modified spectral gravity forward modelling is a spectral technique to deliver near- and/or far-zone gravity effects implied by topographic masses, the shape of which is given as a surface spherical harmonic series. From the numerical point of view, one of its most difficult parts is the accurate computation of the associated Molodensky's truncation coefficients. This is because this evaluation may necessitate to extend the number of significant digits from 16 (double precision) to, say, 64 or even 256. Here, this was achieved using the MATLAB's ADVANPIX toolbox.

MATLAB routines to compute the truncation coefficients and their radial and horizontal derivatives are also available from the link above. The ADVANPIX toolbox is required to run the codes.

Available are also some pre-computed ready-to-use near-zone and far-zone truncation coefficients from the Bucha et al. (2019) study. The coefficients are evaluated for

• the spherical distance of $\psi_0 = 100000\ \mathrm{m}\ /\ 6378137\ \mathrm{m}$ (100 km integration radius from the evaluation point),
• the reference sphere having the radius $R = 6378137\ \mathrm{m}$,
• the radius of the evaluation point $r = 6378137\ \mathrm{m} + 7000\ \mathrm{m}$,
• harmonic degrees $n = 0,\dots,21600$,
• topography powers $p = 1,\dots,30$,
• radial derivatives $k = 0,\dots,40$,
• the first- and second-order horizontal derivatives.

256 significant digits were used to compute the truncation coefficients, ensuring 24-digit accuracy or better. After the evaluation, the coefficients were converted to double precision with 16 significant digits. Importantly, in some cases, the loss of significance errors may be encountered during the spherical harmonic synthesis when using the coefficients (see the reference below).

Please use the following reference when using either the codes or the coefficients:

Bucha, B., Hirt, C., Kuhn, M., 2019. Cap integration in spectral gravity forward modelling up to the full gravity tensor. Journal of Geodesy, https://doi.org/10.1007/s00190-019-01277-3.

SRBF_package

OVERVIEW
--------
Name: SRBF_package
Description: Routines for gravity field modelling with spherical radial basis functions
Programming Languages: Fortran (+ Python wrapper), MATLAB
Download: https://github.com/blazej-bucha/srbf-package

SRBF_package is a collection of a few routines for gravity field modelling with band-limited spherical radial basis functions (SRBFs), allowing both analysis and synthesis of the gravitational field. Harmonically analysed can be the gravitational potential (or any other continuous scalar function on a 2D sphere), while synthesis is possible for the gravitational potential, the gravitational vector in LNOF and the gravitational tensor in LNOF. To our knowledge, the equations to synthesize the gravitational tensor are novel and are more efficient than other formulae (e.g., that from Appendix of Bucha et al., 2016). This is because only three radial basis functions are needed to compute six unique elements of the gravitational tensor. This may improve the computational speed, as the evaluation of band-limited spherical radial basis functions (the sum over harmonic degrees) is the most time-consuming part of the synthesis.

As an example of a band-limited SRBF, the figure below depicts the smoothed Shannon SRBF.

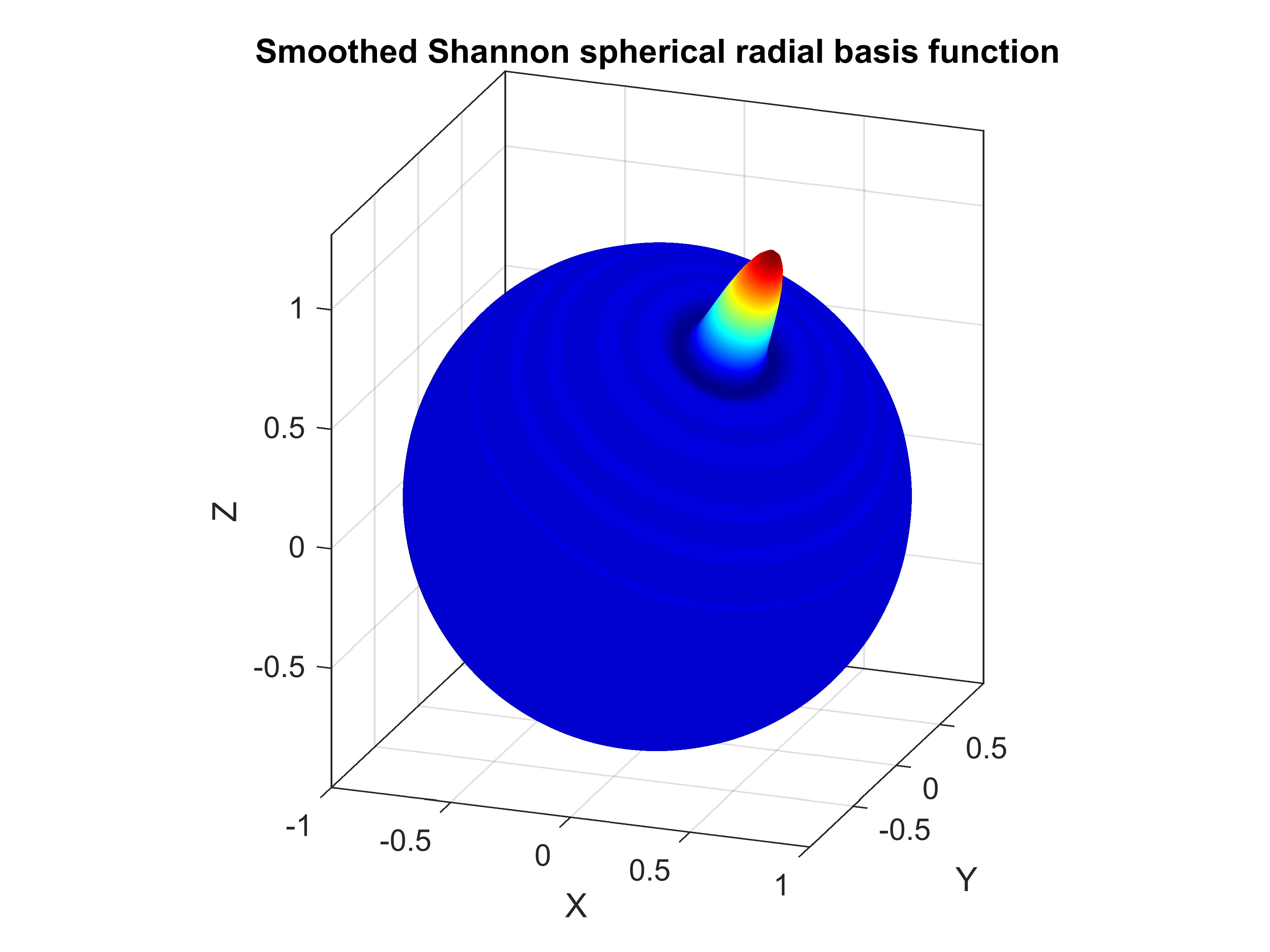
The package is an enhanced version of the MATLAB-based routines used by Bucha et al. (2016). It is available as MATLAB-based functions and Fortran 95 routines accompanied by a Python wrapper. The MATLAB synthesis is parallelized using "parfor" and the Fortran synthesis and analysis are parallelized using OpenMP (the "!$OMP PARALLEL DO" directive). When using the same number of CPUs, the Fortran routines can be up to about 10 times faster than their MATLAB-counterparts. The Python wrapper allows an easy access to the Fortran routines for Python users.

Attached to the package are also also test data, manuals with a detailed description of the package and scripts with two test computations to verify the correctness of the implementation in MATLAB, Fortran and Python. While the test examples are based on global gravity field modelling for clarity, SRBF_package was developed primarily for regional applications with a residual gravity field. This is because SRBF_package is significantly slower when compared to FFT-based SHS and SHA, both of which are designed for global applications. Although the package was designed mainly for gravity field modelling, other applications are possible. Further details can be found in the attached PDF.

Please use the following reference when using SRBF_package:

Bucha, B., Janák, J., Papčo, J., Bezděk, A., 2016. High-resolution regional gravity field modelling in a mountainous area from terrestrial gravity data. Geophysical Journal International 207, 949-966, http://doi.org/10.1093/gji/ggw311.

GMSQ2019

GMSQ2019 is a Gravimetric Model of the Slovak Quasigeoid at 2 arc-sec spatial resolution. It is developed from a high-resolution regional gravity field model (Bucha et al. 2016), which relies on gravity information from (i) EIGEN-6C4 up to degree 2190 (~9 km resolution), (ii) dense terrestrial gravity data modelled by spherical radial basis functions up to degree 21600 (~30 arc-sec), and (iii) residual terrain modelling (~2 arc-sec).

A validation of GMSQ2019 based on 34 high-quality GNSS/levelling data revealed a standard deviation of 1.9 cm. When including reference data of worse quality (but higher quantity, in total 8838), the standard deviation reaches 4.3 cm and a systematic bias of -0.5 m is observed.

The development of GMSQ2019 is discussed in detail in a technical report (in Slovak), which is freely available at https://www.geoportal.sk/files/gz/bucha-et-al-2019-gmsq2019-technicka-sprava.pdf (~17 MB). Further technicalities are provided in the Bucha et al. (2016) paper. GMSQ2019 in 6 arc-sec spatial resolution is shown in the figure below (units are metres, figure size is ~2.8 MB). A figure at the original 2 arc-sec resolution is provided in the technical report (Obr. 1).

grav-sr-2arcsec

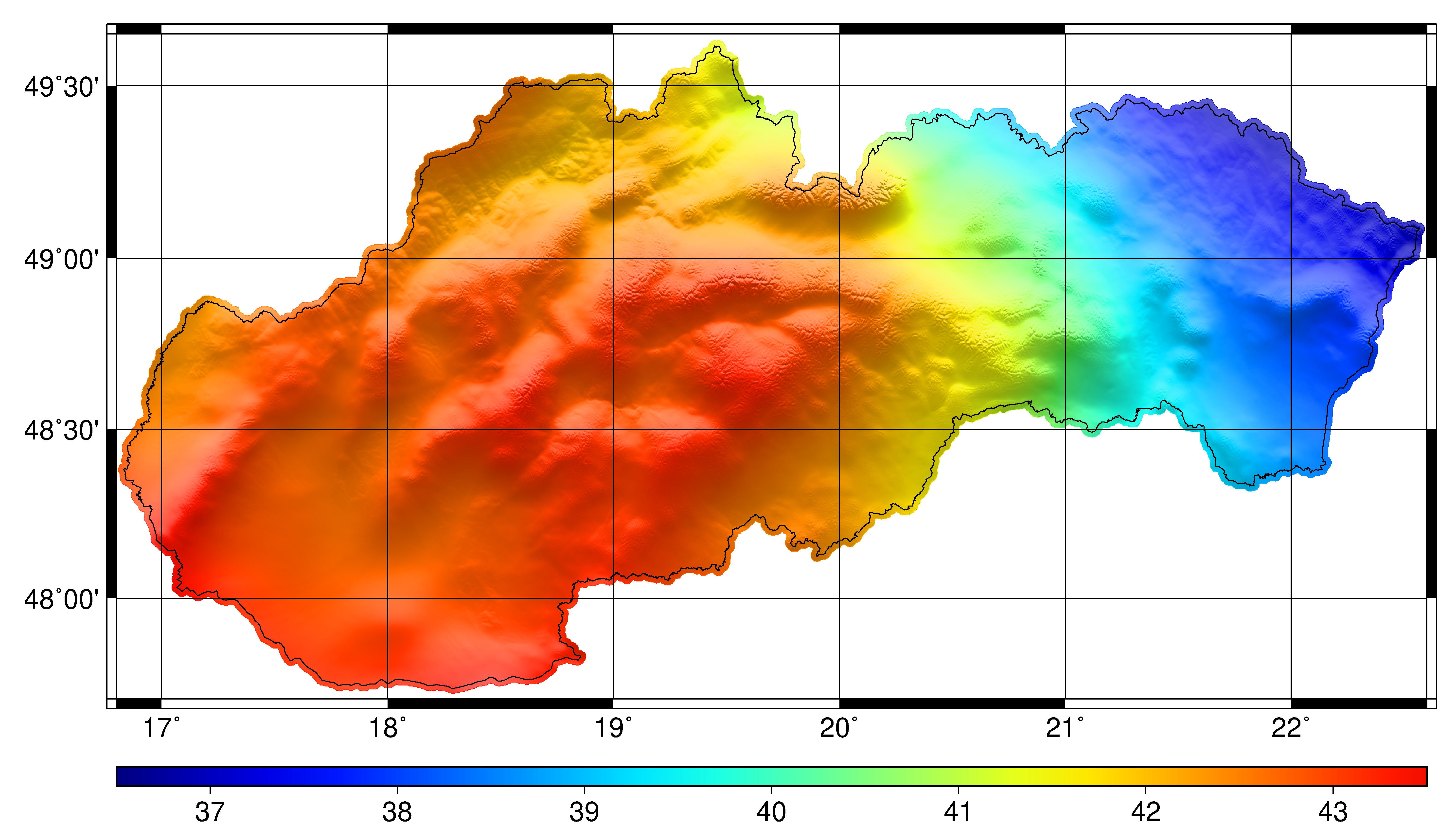
OVERVIEW
--------
Name: grav-sr-2arcsec
Description: 2-arcsec surface gravitational maps of the Slovak Republic
Version: 1.0
Download: https://doi.org/10.5281/zenodo.7074772

grav-sr-2arcsec is a suite of 2-arcsec surface gravitational maps of the Slovak Republic in terms of

• the gravitational potential ($V$),
• the full gravitational vector ($V_x$, $V_y$, $V_z$) in the local north-oriented reference frame (LNOF), and
• the full gravitational tensor in LNOF ($V_{xx}$, $V_{xy}$, $\dots$, $V_{zz}$).

Below is shown the $V_{zz}$ element of the gravitational tensor over the High and Low Tatra Mountains, representing the roughest part of Slovakia.

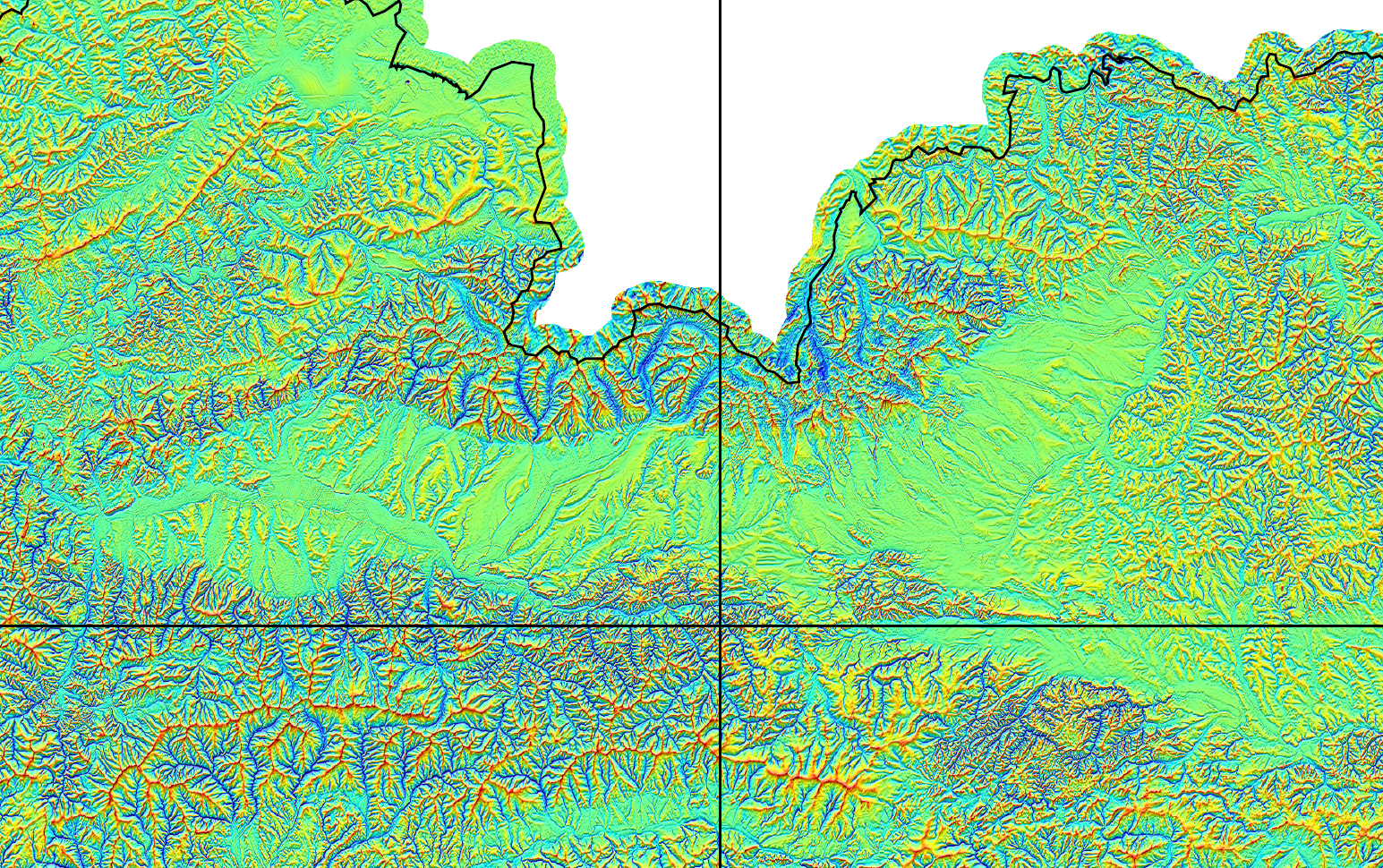
The next figure shows the $V_y$ element of the gravitational vector over the more or less same region.

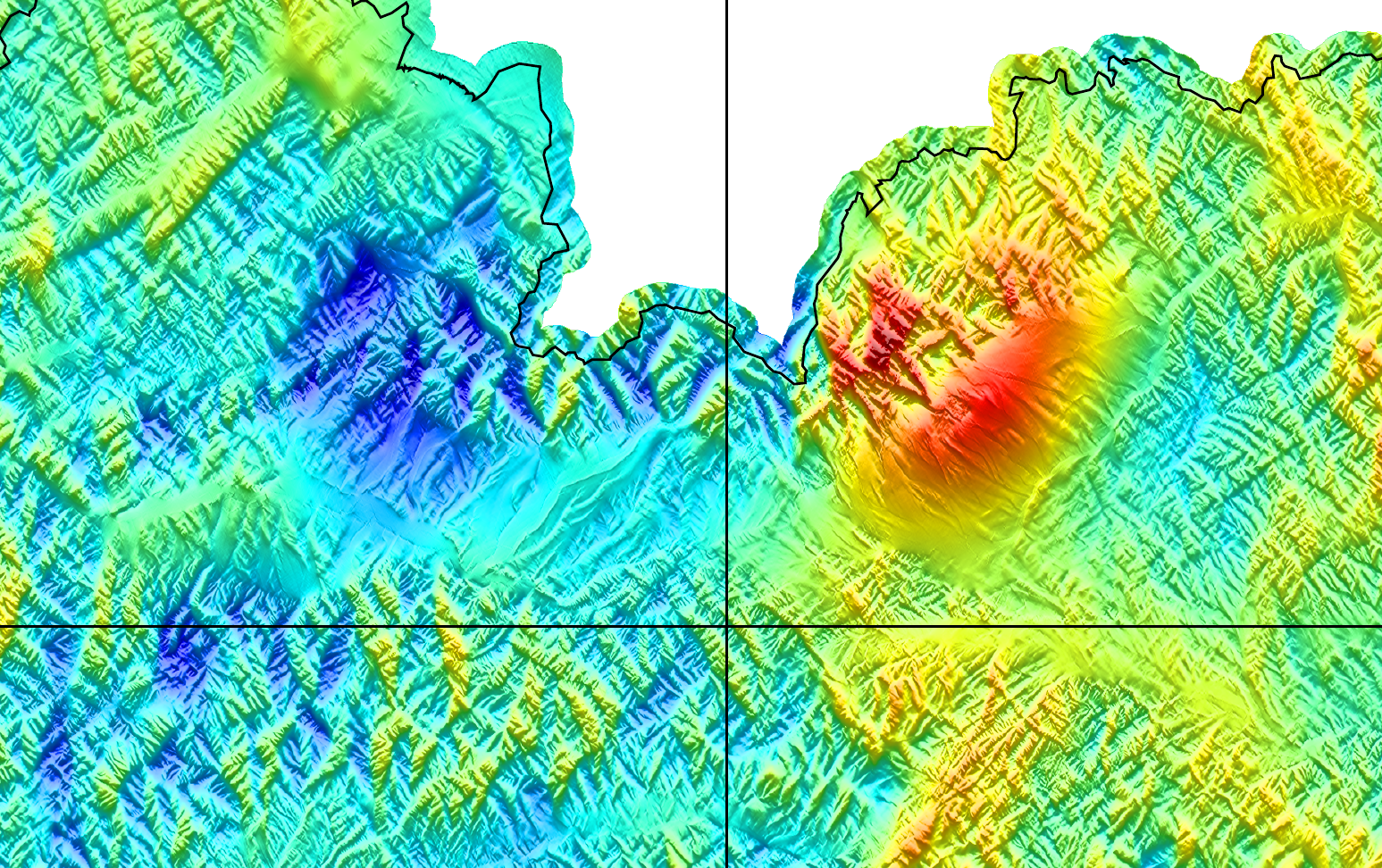
High-resolution figures of the entire grids can be found for all ten quantities in the "figs" directory at link above (more than 30 MB per figure).

The suite was computed from a high-resolution gravity field model of Slovakia developed by Bucha et al. (2016). The maps rely on three sources of gravitational information:

• the Zero-Tide version of the global geopotential model EIGEN-6C4 (Forste, C. et al., 2014) up to degree 2190 (~5 arcmin resolution, ~9 km),
• the expansion of the residual gravitational signal up to degree 21600 in terms of spherical radial basis functions (Bucha et al. 2016) (~30 arcsec, ~950 m), and
• residual terrain modelling (Bucha et al. 2016) (2 arcsec, ~60 m).

An independent validation of grav-sr-2arcsec revealed the standard deviation of 0.789 mGal in terms of the gravity.

Since the residual terrain modelling technique is based on the constant-mass density assumption, grav-sr-2arcsec must *not* be geophysically interpreted at resolutions higher than ~30 arcsec (~950 m). This is because this information comes solely from the shape of the topography and a constant mass density, so the effect of anomalous densities is *not* captured beyond the ~30 arcsec resolution. In the case of the combination "EIGEN-6C4" + "residual terrain modelling" (that is, no spherical radial basis functions), the geophysically relevant information can be found only up to the resolution of EIGEN-6C4, that is, ~9 km. Nevertheless, the residual terrain modelling grids are still very useful for improving the accuracy with respect to independent ground-truth (e.g., observed terrestrial gravity).

Unfortunately, due to the license restrictions, the gravitational information captured by spherical radial basis functions is not allowed to be published as user-friendly grids. The information is, however, provided in terms of expansion coefficients of spherical radial basis functions, so that one can *exactly* reproduce their contribution, avoiding any approximations (attached is an efficient ready-to-use Fortran program that will do the work for you).

To name a few possible applications:

• screening observed terrestrial gravity for possible outliers,
• reduction of observed terrestrial gravity from the sensor height down to the ground level,
• computation of gravity anomalies/disturbances, deflections of the vertical, disturbing tensor, etc.,
• geoid/quasigeoid determination,
• accurate reduction of observed horizontal angles to a cartographic projection using deflections of the vertical,
• investigations of the curvature of plumb lines,
• geophysical interpretations,
• educational purposes — from elementary schools (Kids, what is the gravitational field, anyway? Do you know how the gravitational field looks like? By investigating the maps, can you say whether the gravitational field is strong or weak in your town/village? In which place in Slovakia does the gravitational field pull you downward the most? Etcetera, etcetera, etcetera) to universities,
• and perhaps many more.

If you use the grav-sr-2arcsec suite, I will be happy if you let me know about your application!

The core data (~6.5 GB) are provided as HDF5 data files, which can be read in many commonly used programming languages. Further informations on grav-sr-2arcsec can be found in the attached README.txt file.

GFM_DE_rule package

OVERVIEW
--------
Name: GFM_DE_rule
Description: Spatial-domain gravity forward modelling
Programming Language: Fortran, MATLAB
Download: https://github.com/blazej-bucha/gfm-de-rule

The GFM_DE_rule package computes the gravitational potential of a body, the shape of which is given by a surface spherical harmonic expansion and the density of which is constant. The evaluation points can be located inside the body, on its surface or outside the body.

The package builds on the spatial-domain gravity forward modelling technique developed by Fukushima (2017). It evaluates the Newton integral in the spatial domain via the double exponential rule. The Fortran routines from that paper are utilized, while several modifications were necessary to fit the goals of the package.

The package is written in Fortran and MATLAB. The Fortran version supports computations in double as well as quadruple precision and is generally faster than the MATLAB version.

The accuracy of the output potential can reach 14 correct digits in double precision and ~30 digits in quadruple precision. The accuracy level is controlled via a relative tolerance error parameter. The higher the required accuracy, the longer the computation times can be expected. The package was designed mainly for modelling gravitational fields of bodies with shapes expanded to low-degree surface spherical harmonic series.

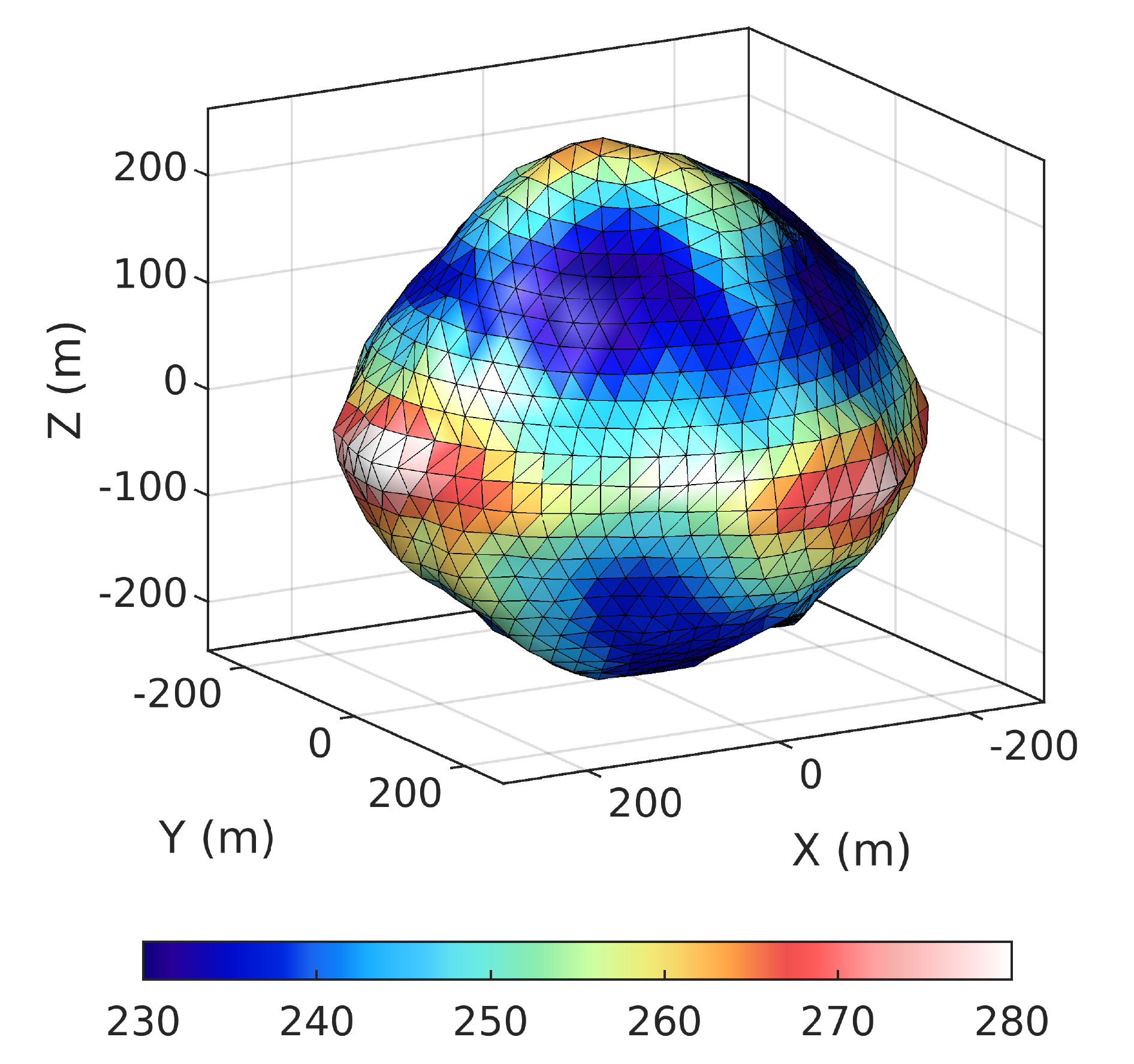
As an example, below are shown respectively degree-15 surface spherical harmonic expansion of shape of the asteroid Bennu (units are metres) and the implied surface gravitational potential ($\mathrm{m}^2 \, \mathrm{s}^{-2}$). At 99.4 % of the grid points, the gravitational potential is computed correctly up to the 14th digit. The figures are due to Bucha and Sanso (2021). The data used to prepare the figures can be found in the Asteroid (101955) Bennu and its gravitational field section.

Asteroid Bennu and its gravitational field

OVERVIEW
--------
Description: Dataset from the Bucha and Sanso (2021) study
Dataset Download: https://doi.org/10.5281/zenodo.6622624

In Bucha and Sanso (2021), we investigated three spherical-harmonic-based techniques to deliver external gravitational field models of the asteroid (101955) Bennu within its circumscribing sphere. This region is known to be peculiar for external spherical harmonic expansions, because it may lead to a divergent series. The studied approaches are

• spectral gravity forward modelling via external spherical harmonics,
• the least-squares estimation from surface gravitational data using external spherical harmonics, and
• the combination of internal and external series expansions.

While the first method diverges beyond any reasonable doubts, we show that the other two methods may ensure relative accuracy from ${\sim}10^{-6}$ to $10^{-8}$ in the vicinity of Bennu. This is possible even with the second method, despite the fact that it relies on a single series of external spherical harmonics. Our main motivation was to study conceptual differences between spherical harmonic coefficients from satellite data (analogy to the first method) and from surface gravitational data (the second method). Such coefficients are available through the popular spherical-harmonic-based models of the Earth's gravitational field and often are combined together. We show that the coefficients from terrestrial data may lead to a divergence effect of partial sums, though excellent accuracy can be achieved when such model is used in full. Under (presently) extreme but realistic conditions, the divergence effect of partial sums may affect many near-surface geoscientific applications, such as the geoid/quasigeoid computation or residual terrain modelling.

The dataset is available at the link above. Next follows a brief description.

Surface spherical harmonic coefficients of Bennu's shape

The shape surface spherical harmonic coefficients of Bennu are provided up to maximum harmonic degree 15 and were computed from a polyhedral shape model. The physical model of Bennu was obtained after assigning a single-constant mass density of $\rho = 1260\ \mathrm{kg} \, \mathrm{m}^{-3}$ to this shape. A figure of the synthesized shape of Bennu is provided in the GFM_DE_rule section above. The original polyhedral model is shown below (colour bar in meters, Bucha and Sanso, 2021).

Spectral gravity forward modelling using external spherical harmonics

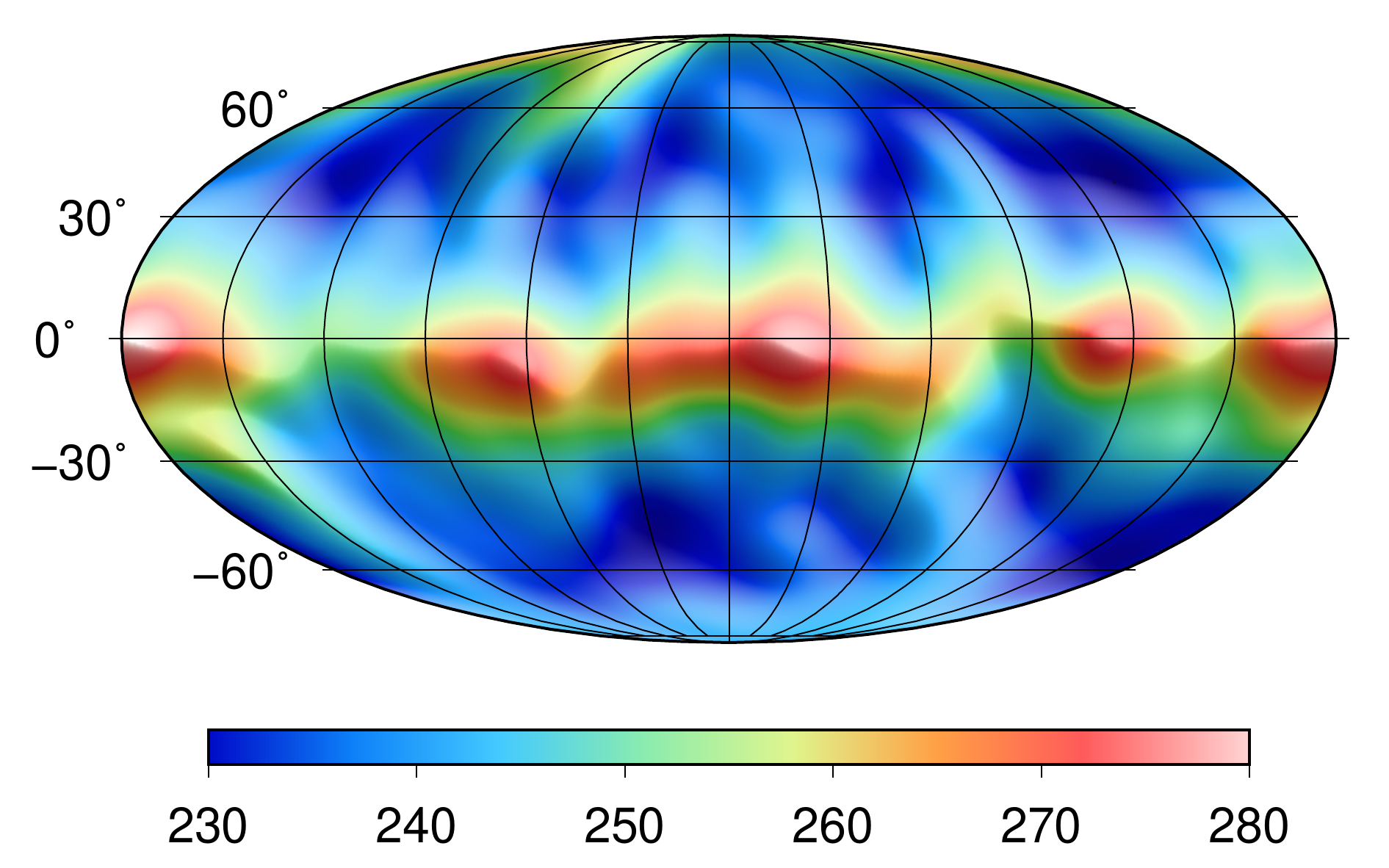
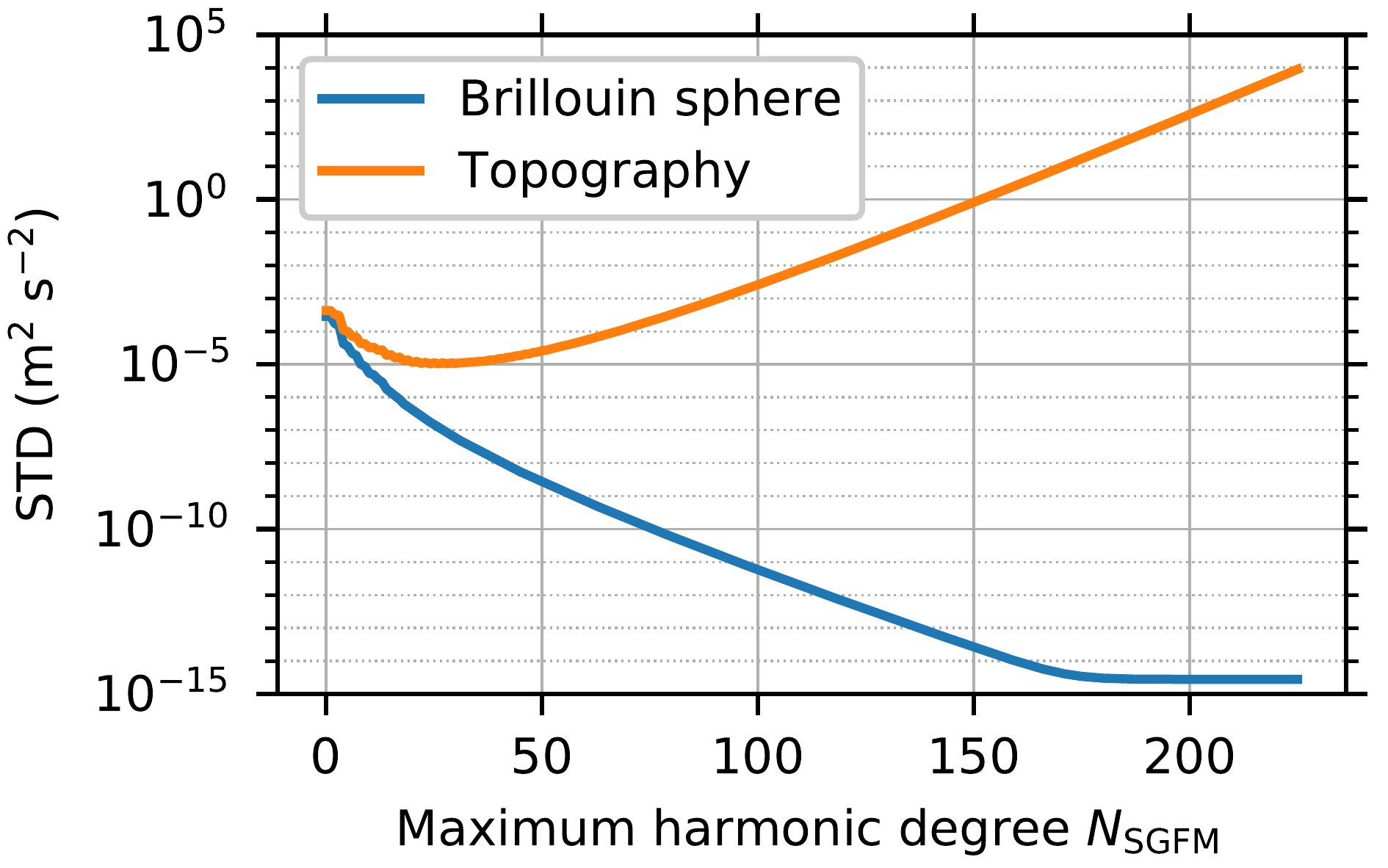
Using the degree-15 shape expansion of Bennu and assuming a constant-mass density, we computed spherical harmonic coefficients of the external gravitational potential using spectral gravity forward modelling. The maximum degree of the potential coefficients is 225. On a Brillouin sphere, they reproduce the gravitational potential with a 14-digit accuracy or better. However, on/below the sphere of convergence, including the surface of Bennu, the spherical harmonic series diverges and produces grossly invalid results. The figure below shows the standard deviations of the errors of the model as a function of maximum harmonic degree (Bucha and Sanso, 2021).

Least-squares estimation from surface gravitational data using external spherical harmonics

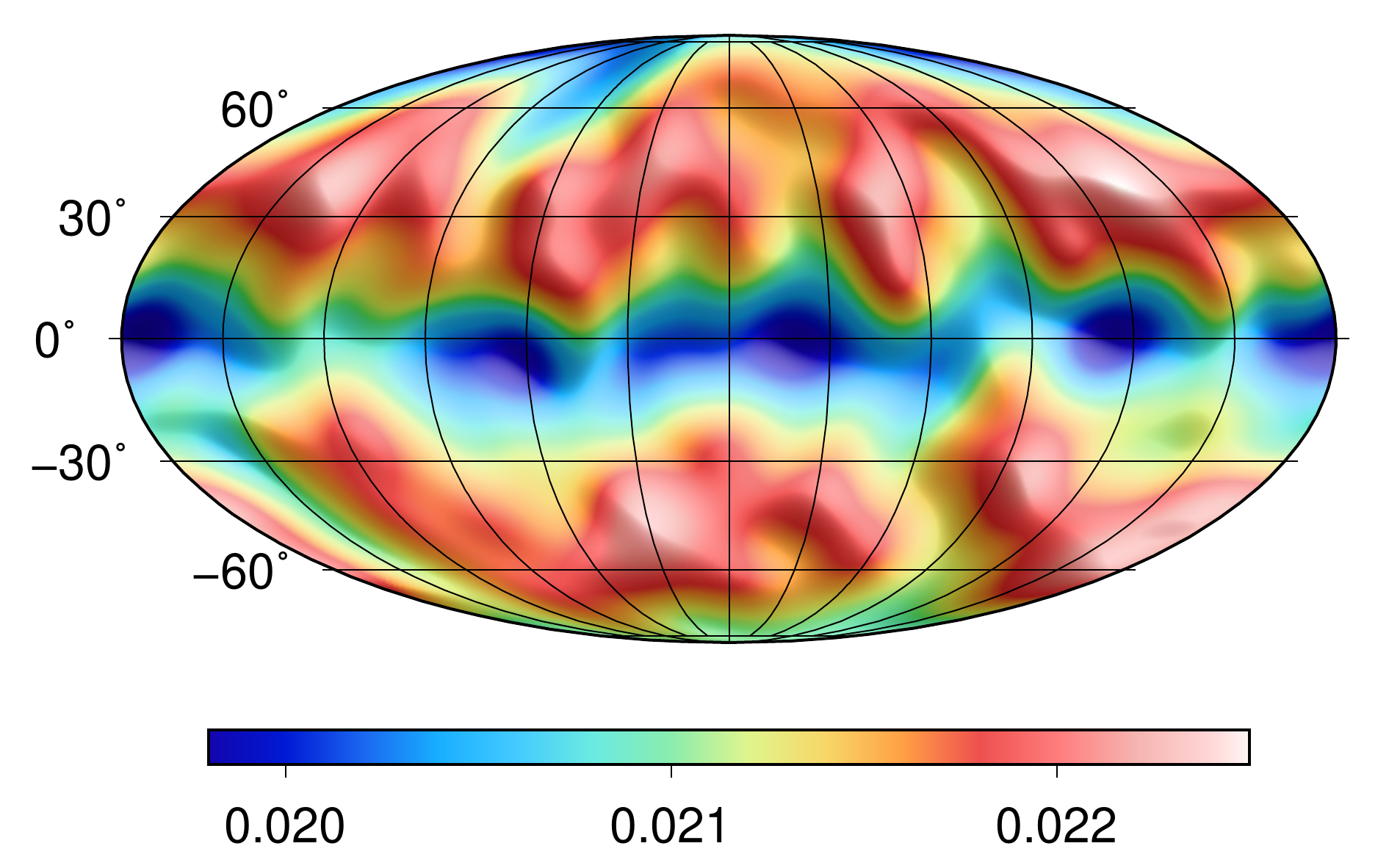
To allow for an accurate spherical-harmonic-based gravitational field modelling everywhere on and above the surface of Bennu while still relying on external spherical harmonics, we developed models from surface gravitational data using the least-squares estimation. These models rely on the Runge—Krarup theorem and provide an $\varepsilon$-accuracy, $\varepsilon > 0$, everywhere on and above Bennu. In our case, they outperform spectral gravity forward modelling on the surface of Bennu by more than 3 orders of magnitude (relative accuracy is ${\sim}10^{-6}$; Bucha and Sanso, 2021). The models were estimated up to maximum degrees 0, 5, 10, ..., 65. The figure below validates them on the surface of Bennu; the solid colour lines represent standard deviations of the errors of the least-squares models and the dashed black line represents spectral gravity forward modelling.

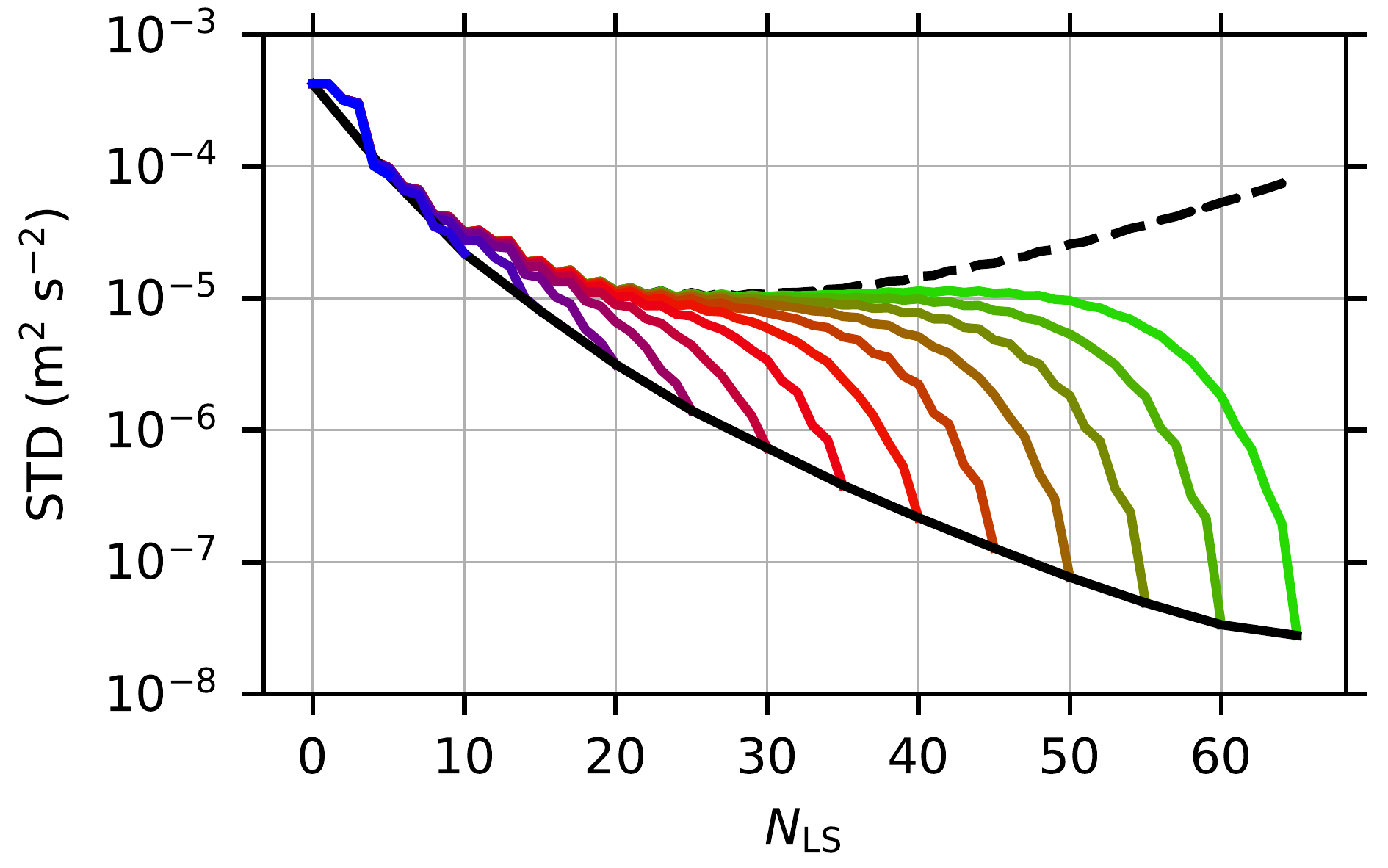
The computation of the models took 90 CPU years.

Combination of internal and external series expansions

Finally, spherical harmonic coefficients of the internal and external series expansions were computed. They do not suffer from the divergence, but their usage on the surface of Bennu is less straightforward as with external spherical harmonics. The figure below (Bucha and Sanso, 2021) shows the accuracy levels achieved with spectral gravity forward modelling (the orange curve), least-squares method (green) and the combination of internal and external series expansions (blue) as a function of harmonic degree.

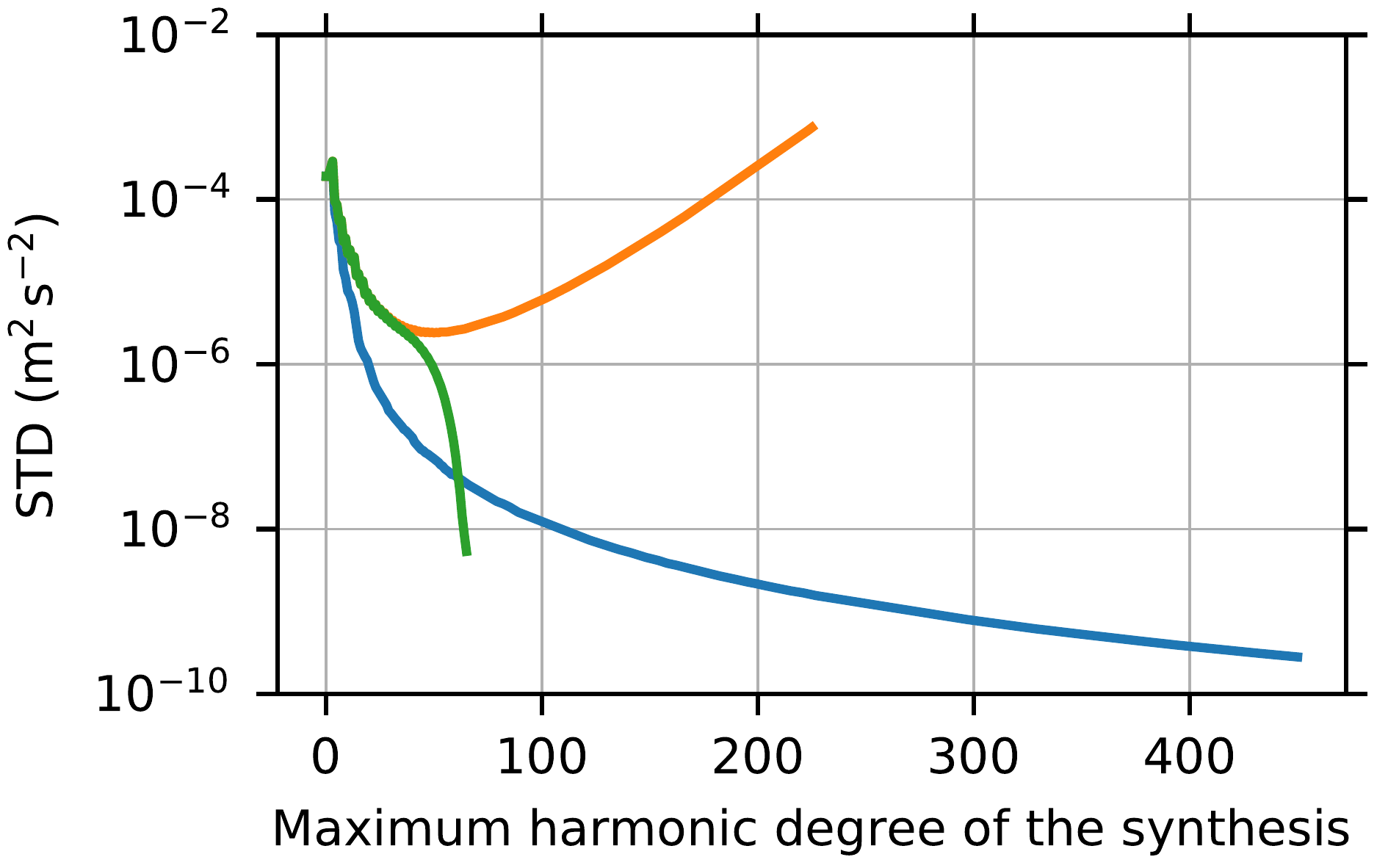
Reference gravitational data

Reference gravitational data (accurate up to the 14th digit) on a Brillouin sphere, a mean sphere and the surface of Bennu are also available. The data were computed using the GFM_DE_rule package. The surface potential is shown in the GFM_DE_rule section above.

Publications

• Sanso, F., Bucha, B., 2023. Change of boundary: towards a mathematical foundation of global gravity models. Journal of Geodesy, 97, 63 https://doi.org/10.1007/s00190-023-01748-8, Open Access


• Bucha, B., 2022. Spherical harmonic synthesis of area-mean potential values on irregular surfaces. Journal of Geodesy, 96, 68 https://link.springer.com/article/10.1007/s00190-022-01658-1, free full-text view-only version available


• Kuna, M., Novák, D., Bucha Rášová, A., Bucha, B., Machová, B., Havlice, J., John, J., Chvojka, O., 2022. Computing and testing extensive total viewsheds: a case of prehistoric burial mounds in Bohemia. Journal of Archaeological Science, 142, 105596, https://doi.org/10.1016/j.jas.2022.105596


• Bucha, B., Rossi, L., Sanso, F., 2021. Error bounds for the spectral approximation of the potential of a homogeneous almost spherical body. Studia Geophysica et Geodaetica, 65, 235-260, https://link.springer.com/article/10.1007/s11200-021-0730-4, Open Access


• Bucha, B., Sanso, F., 2021. Gravitational field modelling near irregularly shaped bodies using spherical harmonics: a case study for the asteroid (101955) Bennu. Journal of Geodesy, 95, 56, https://link.springer.com/article/10.1007/s00190-021-01493-w, free full-text view-only version available


• Bucha, B., Kuhn, M., 2020. A numerical study on the integration radius separating convergent and divergent spherical harmonic series of topography-implied gravity. Journal of Geodesy 94, 112, https://link.springer.com/article/10.1007/s00190-020-01442-z, free full-text view-only version available


• Bucha, B., Hirt, C., Yang, M., Kuhn, M., Rexer, M., 2019. Residual terrain modelling (RTM) in terms of the cap-modified spectral technique: RTM from a new perspective. Journal of Geodesy 93, 2089-2108, https://doi.org/10.1007/s00190-019-01303-4, free full-text view-only version available


• Hirt, C., Bucha, B., Yang, M., Kuhn, M., 2019. A numerical study of residual terrain modelling (RTM) techniques and the harmonic correction using ultra-high-degree spectral gravity modelling. Journal of Geodesy 93, 1469-1486, https://doi.org/10.1007/s00190-019-01261-x, free full-text view-only version available


• Bucha, B., Hirt, C., Kuhn, M., 2019. Cap integration in spectral gravity forward modelling up to the full gravity tensor. Journal of Geodesy 93, 1707-1737, https://doi.org/10.1007/s00190-019-01277-3, free full-text view-only version available


• Hirt, C., Yang, M., Kuhn, M., Bucha, B., Kurzmann, A., Pail, R., 2019. SRTM2gravity: An Ultrahigh Resolution Global Model of Gravimetric Terrain Corrections. Geophysical Research Letters 46, 4618-4627, https://doi.org/10.1029/2019GL082521, free full-text view-only version available


• Bucha, B., Hirt, C., Kuhn, M., 2019. Divergence-free spherical harmonic gravity field modelling based on the Runge—Krarup theorem: a case study for the Moon. Journal of Geodesy 93, 489-513, https://doi.org/10.1007/s00190-018-1177-4, free full-text view-only version available


• Bucha, B., Hirt, C., Kuhn, M., 2019. Cap integration in spectral gravity forward modelling: near- and far-zone gravity effects via Molodensky's truncation coefficients. Journal of Geodesy 93, 65-83, https://doi.org/10.1007/s00190-018-1139-x, free full-text view-only version available


• Rexer, M., Hirt, C., Bucha, B., Holmes, S., 2018. Solution to the spectral filter problem of residual terrain modelling (RTM). Journal of Geodesy 92, 675-690, https://doi.org/10.1007/s00190-017-1086-y, free full-text view-only version available


• Bucha, B., Janák, J., Papčo, J., Bezděk, A., 2016. High-resolution regional gravity field modelling in a mountainous area from terrestrial gravity data. Geophysical Journal International 207, 949-966, http://doi.org/10.1093/gji/ggw311


• Bucha, B., Bezděk, A., Sebera, J., Janák, J., 2015. Global and regional gravity field determination from GOCE kinematic orbit by means of spherical radial basis functions. Surveys in Geophysics 36, 773-801, http://doi.org/10.1007/s10712-015-9344-0, free full-text view-only version available


• Kostelecký, J., Klokočník, J., Bucha, B., Bezděk, A., Förste, Ch., 2015. Evaluation of gravity field model EIGEN-6C4 by means of various functions of gravity potential, and by GNSS/levelling. Geoinformatics FCE CTU, http://dx.doi.org/10.14311/gi.14.1.1


• Bucha, B., Janák, J., 2014. A MATLAB-based graphical user interface program for computing functionals of the geopotential up to ultra-high degrees and orders: Efficient computation at irregular surfaces. Computers & Geosciences 66, 219-227, http://doi.org/10.1016/j.cageo.2014.02.005


• Bucha, B., Janák, J., 2013. A MATLAB-based graphical user interface program for computing functionals of the geopotential up to ultra-high degrees and orders. Computers & Geosciences 56, 186-196, http://doi.org/10.1016/j.cageo.2013.03.012

Preprints are available at my ResearchGate profile. For some of the papers above, free full-text view-only versions are available.

Presentations

• Bucha, B., Kuhn, M., 2023. Integration radius as a parameter separating convergent and divergent spherical harmonic series of topography-implied gravity. IUGG, the 28th General Assembly, 11--20 July, Berlin, presentation, https://doi.org/10.57757/IUGG23-0423.


• Bucha, B., Sanso, F., 2023. Satellite and terrestrial spherical harmonic coefficients of the external gravitational potential do not match. EGU General Assembly, 23--28 April, Vienna, EGU23-6147, presentation.


• Bucha, B., 2022. 10 years with spherical harmonics. Tatry 2022, Globálna geodezia a geoinformatika, 24--25 November, Štrbské Pleso, Slovakia, presentation.


• Bucha, B., 2022. Integral of solid spherical harmonic expansions at grid cells residing on undulated surfaces. The X. Hotine--Marussi Symposium, 13--17 June, Milan, presentation.


• Bucha, B., 2022. CHarm: C library to work with spherical harmonics up to almost arbitrarily high degrees. EGU General Assembly, 23--27 May, Vienna, EGU22-11206, presentation.


• Klokočník, J., Kostelecký, J., Pešek, I., Bezděk, A., Bucha, B., 2016. On feasibility to detect volcanoes hidden under ice of Antarctica via their "gravitational signal". EGU General Assembly, 17--22 April Vienna, Austria, Geophysical Research Abstracts, Vol. 18, EGU2016-2815.


• Bucha, B., Bezděk, A., Janák, J., 2015. An approach to stabilize the estimation of global GOCE-only gravity field models from kinematic orbit in terms of spherical radial basis functions. Geodetické základy a geodynamika, 8--9 October, Kočovce, Slovakia. ISBN: 978-80-227-4466-9.


• Kostelecký, J., Klokočník, J., Bucha, B., Bezděk, A., Förste, Ch., 2015. Evaluation of EIGEN-6C4 by means of various functions of the gravity potential, and by GPS/Leveling EGU General Assembly, Vienna, Austria, 12--17 April, Geophysical Research Abstracts, Vol. 17, EGU2015-3910.


• Bucha, B., Bezděk, A., Janák, J., 2014. Global gravity field determination from kinematic orbits of CHAMP, GRACE and GOCE satellites by means of spherical radial basis functions. Geomatika v projektech 2014, Zámek Kozel, 1--2 October, ISBN: 978-80-263-0796-9.

Posters

• Bucha, B., 2023. Spectral gravity forward modelling of continuous 3D mass density distributions. AGU23, 11--15 December, San Francisco, California, USA.

Teaching

• Bucha, B., 2023. Fyzikálna geodézia [Physical Geodesy]. 1st edn. Spektrum STU, Bratislava, p 184. ISBN 978-80-227-5368-5.
  
  The final published version is available at https://www.svf.stuba.sk/buxus/docs/dokumenty/skripta/2023/Fyzikalna_geodezia.pdf under the CC BY 4.0 license.
  The source code is available at https://github.com/blazej-bucha/physical-geodesy-lecture-notes under the BSD-3-Clause license.

Favourite websites

• http://icgem.gfz-potsdam.de/home—International Centre for Global Earth Models, the website offers a large pallet of spherical harmonic gravity field models of the Earth and of other celestial objects, such as the Earth's Moon, Mars, etc.


• http://www.asu.cas.cz/~bezdek/—Website of Aleš Bezděk with gravity field models from GPS tracking and a MATLAB script for 3D visualizing geodata on a rotating globe


• http://www.fftw.org/—Fastest Fourier Transform in the West, a C library for discrete FFTs


• https://lwn.net/Articles/250967/—Find and fix bottlenecks related to memory in your programs. This can lead to drastic improvements in speed execution. PDF at https://people.freebsd.org/~lstewart/articles/cpumemory.pdf.


• https://dl.acm.org/doi/10.1145/103162.103163—Great source of information on floating point arithmetic.


• https://www.rce-cast.com/—Podcast on high-performance computing, interviews with developers of FFTW, NetCFD, NumPy and many other numerical libraries


• http://www.kaeg.sk/vyskum/projekty-apvv/apvv-0194-10-bouguer_ng/— 250 x 250 m grid of complete Bouguer anomaly over Slovak Republic and a program for terrain corrections calculations


• http://www.math.sk/gbvp/— Colleagues from the Department of Mathematics and Descriptive Geometry, STU Bratislava, who work on numerical solutions to geodetic boundary value problems


• https://www.researchgate.net/profile/Toshio_Fukushima—ResearchGate profile of Prof. Toshio Fukushima with dozens of state-of-the-art algorithms for gravity field modelling